 |
| Foundations of Transcomplex Numbers. |
Is there no end to this? Is there no "final" type of numbers?
From the standpoint of number fields, all of them can be encompassed into one type called the complex number field.
Wikipedia, in a short background, mentions how the complex numbers emerged:
Complex numbers were first conceived and defined by the Italian mathematician Gerolamo Cardano, who called them "fictitious", during his attempts to find solutions to cubic equations. The solution of a general cubic equation may require intermediate calculations containing the square roots of negative numbers, even when the final solutions are real numbers, a situation known as casus irreducibilis. This ultimately led to the fundamental theorem of algebra, which shows that with complex numbers, a solution exists to every polynomial equation of degree one or higher.Complex numbers can also be understood and developed from the standpoint of view of ordered pairs. Today, developing the complex number system from the foundations of set theory and the concept of ordered pairs is possibly the most intuitive approach we have at hand.
For a rigorous development of the complex number system download the free EBook: Foundations Of Transcomplex Numbers: An Extension Of The Complex Number System To Four Dimensions.
This mathematics book is about a way of extending the complex numbers system to four-coordinate variables, maintaining the usual operations attributed to the complex numbers.Foundations ... is a fully illustrated EBook. See --and Click-- for example, the following figure about how to multiply two ordered pairs:
 |
| Transcomplex numbers are an extension of the common complex numbers. |
In a nutshell, transcomplex numbers are complex numbers whose elements are ordered pairs.
In the following simple illustration, also taken from Foundations ... we can see that out of a four-entry complex number system we can extract four 3-dimensional spaces like "ours".
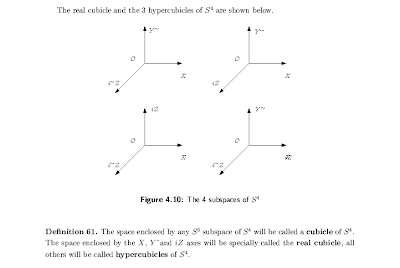 |
| The transcomplex numbers need a 4-dimensional coordinate system to be represented. |
- Ordered Pairs. The whole theory of transcomplex functions is based on the ordered pair concept: from the two-dimension plane up to the four-dimension space.
- Complex Numbers. The complex numbers system is derived from the ordered pair's concept.
- Transcomplex Numbers. Here starts the extension of the complex numbers into ordered pairs of complex numbers, arriving at the concept of transcomplexs.
- The Coordinate System S4. This chapter is devoted to deriving a suitable coordinate system to plot transcomplex functions.
- Transcomplex Functions. Functions of complex variables evolve to make space for functions of four-entries ordered pairs.
- Transcomplex Surfaces. A radical and totally new perception of surfaces generated by complex variables.
- Theorem Proofs. This chapter collects all the proofs of the theorems stated along the book.