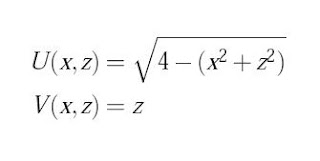This "definition" may sound a little abstract, but a few examples should bring the idea comprehensibly.
When we think about the basic Cartesian coordinate system of two axes, we immediately think of two "real number lines" intersecting at 90 degrees.
 |
| Every plane curve is a set of ordered pairs |
The figure above shows an example of how we intuitively use ordered pairs when we plot graphs of real functions.
In this example, The function is any abstract one-one (1-1) rule Y = f (x). When the variable x on the X-axis assumes or takes the value a, then the function f assigns the value b on the Y-axis to that choice x= a on the X-axis.
Hence, we are necessarily and intuitively talking about the ordered pair (a, b). This entity (a, b) is an ordered pair because the function f explicitly and uniquely assigns the value b to the unique value a.
The notion of ordered pair is not limited to the usage of the real numbers. We can choose the second entry of the ordered pair to be an imaginary number. In that case, the Y-axis is no longer a real-numbers axis, but an imaginary numbers axis. In that case, the ordered pair is simply a complex number.
The ordered pairs are very useful when we deal with transformations, especially transformations of plane figures.
For example, the following transformation made up of two parametric equations:
transforms a circular area of the plane into a dome in space.
To dramatize the results, a picture of a cat is shown before this transformation, and after the parametric equations are applied to the cat's photo.
 |
| A flat image transformed into a 3D-image. |
In this example we are implicitly using triplets, that is, ordered pairs of three entries, like (x, y, z). The first two entries of the triplet are for the locations of the points of the cat's photo, and the third entry of the triplet is for the amount of "deformation" applied to each point of the photo.
Transformations and ordered pairs are very interesting subjects because they are not so abstract after all.
Interested in more examples of transformations as in the example above? Then download this free E-Book:
 |
| The Golden EBook of Graphs of Mathematical Functions. |
Interested in an in-depth development of the foundation of the complex numbers from the standpoint of the ordered pairs?
 |
| Foundations of Transcomplex Numbers. |